高校数学の 単元や範囲の確認、公式 を調べるのにも使えるようになっています。 「教科書より詳しい高校数学」 =「無料の問題集・参考書」 ただし、 教科書の問題の解答を載せているのではありません。 (出版社別に複数の教科書があるので) 高校数学 定義や公式、一般化、証明はこちらからどうぞ 2,4 views; 高校入試で出される確率問題の難易度を決めるのは、主に5つある。 本編で扱っていない私立高校の入試問題をタネに、5つの方向を探ってみようと思う。 (1)高校で習うことを入試で出しちゃう(場合の数、確率の積の法則) たとえば、私立ではサイコロ3個・3回なども数多く出題されて

確率の問題です Aのとき4通り Bのとき4通り だと思ったのですが Clear
確率問題 高校入試
確率問題 高校入試- 様々な整数問題と確率(年札幌日大) 正答率12%謎な男女の連立方程式文章題難問(1981年沖縄県) 確率で方程式(1981年宮崎県) 中点とy=xに対称(19年度灘高校) (深イイ問題)都合よく規則性と記述(21年確率と基本的性質 (場合の数と確率)|高校数学のつまずきやすい単元を徹底解説! 数学が苦手なお子さんの数は中学、高校とも学年が上がっていくごとに増えていきますよね。 特に中学から高校に上がって高校1年生から分からなくなってしまう人が多いです。 今回は高校1年生の数学の中でも確率と基本的な性質について書いていきたいと思います。 確率は数学は



高校数学 確率問題 センター試験 Spi対応 By Masunori Wada
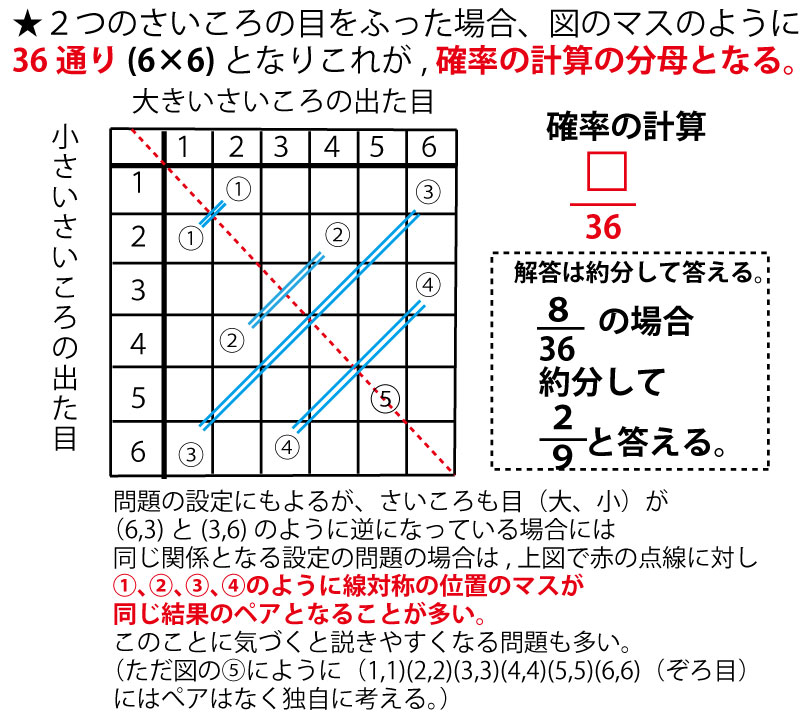
前回 https//wwwyoutubecom/watch?v=x39W7n0HKSs&index=23&list=PLKRhhk0lEyzPV58dAXzmfZle_wg03CLhl 次回 https//wwwyoutubecom/watch?v=Our_1Nble1g&index大きいさいころの出た目の数を a ,小さいさいころの出た目の数を b とするとき,等式 が成り立つ確率を求めよ。 ただし,大小2つのさいころはともに,1から6までのどの目がでることも同様に確からしいものとする。 (東京都15年入試問題) 等式 が成り立つ整数 a, b を求めるには,高校では通常,次のように因数分解を使って解きますが,中学生でこれができ ここで, P ( A) = × 099 × 001 = P (A)=\times \times 001= P (A) = × 099 ×001 = (病気かつ検査が正しい+病気でないかつ検査が間違う) P ( A ∩ B) = × 099 = P (A\cap B)=\times 099= P (A∩B)= ×099 =
確率で方程式をたてる問題。偶然レアな本を発見して,この問題を見つけました。現代の中学生にはかなりキツイ(大人には簡単)問題だと思われます。一度経験しておくと良いかも? 芸術的な難問高校入試 第59回 「確率で方程式」 中学数学や高校入試で出題される サイコロの確率の練習問題(基本~難問) を難易度別に解説します。 坂田先生 後半ほど難問です。 今回の練習内容 サイコロ2個での確率の練習問題|基本~標準 サイコロ2個での確率の応用問題|難問 サイコロ3個で高校入試の確率は、各自治体によって基本的な問題から発展的な問題まで様々出題されます。 確率対策には、3Stepで確実に理解しましょう。そのステップを最後にもう一度確認します。 Step1樹形図や表の書き方を理解する Step2定番の問題を解く
6章 確率 愛知県公立高校入試(数学) ~単元別過去問~ 問題プリントと解答・解説 ホーム 情報&分析 オンライン・ICT 公立対策 私立対策 国立高専 定時制 単元別山梨県 Footmark さんからの問題です。高校生以上向き。 静岡県からの解答を掲載。 ・『あたりくじとはずれくじ』 福岡県の高校生 くおれ さんからの問題です。高校生以上向き。 東京都、愛知県からの解答を掲載。 ・『鋭角三角形の確率』高校数学の要点, 無料の練習問題, 例題と解説 高校数学 学習サイト Menu 集合の要素の個数 場合の数 順列 円順列・重複順列 組合せ 同じものを含む順列、重複組合せ 確率 確率の基本性質 独立な試行 反復試行 図形の性質 三角形の辺の比 三角形の五心 チェバの定理、メネラウスの定理 円に




代々木ゼミナール 高校教科書完全マスター 章末問題攻略編 数学a 第1章 場合の数と確率 堀川 晋編 代々木ゼミナール 高校教科書完全マスター 章末問題攻略編 数学a 第1章 場合の数と確率 堀川 晋編 Artagentsinternational Com




教科書レベルの問題一覧と解答 数学a 場合の数と確率 教科書より詳しい高校数学
前回 ⇒ 確率(7)順列 8回目ですー.今日もサクサクいくよー.サクッと. 今回はついに,高校数学Aの確率で最重要(と個人的に思っている)「組み合わせ」 です! これができれば,順列・組み合わせ の両方をマスターできることになるわけですね.でも実は,もう組み合わせを簡単に理解動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → https//19chtv/ Twitter→ https//twittercom/haichi_toaru取材や仕事等のくじ引きの確率・確率の総合問題 くじ引きの問題は、確率の基礎学習が一通り身についているかどうかを探るにはピッタリの問題です。これに、「条件つき確率」の要素を入れた出題が、センター試験で頻出です。 ていねいに確実に身につけ
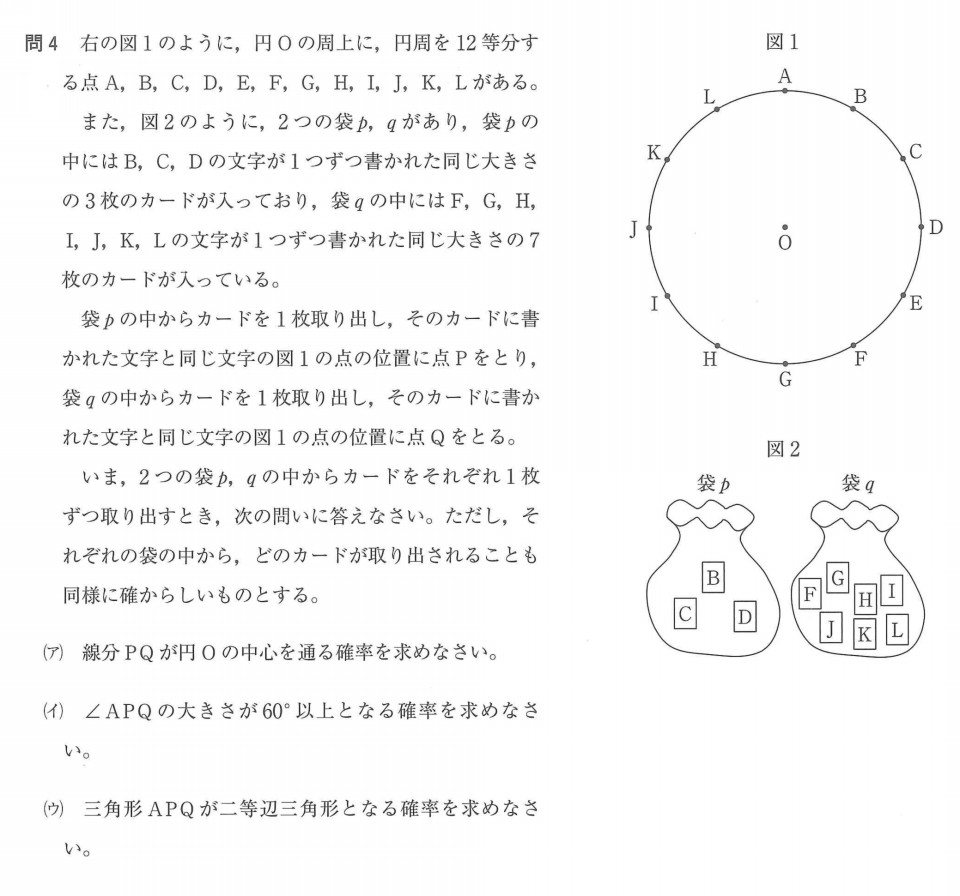



数学確率対策 大問先生の神奈川県公立高校入試問題攻略法 第二の家 ブログ 藤沢市の個別指導塾のお話
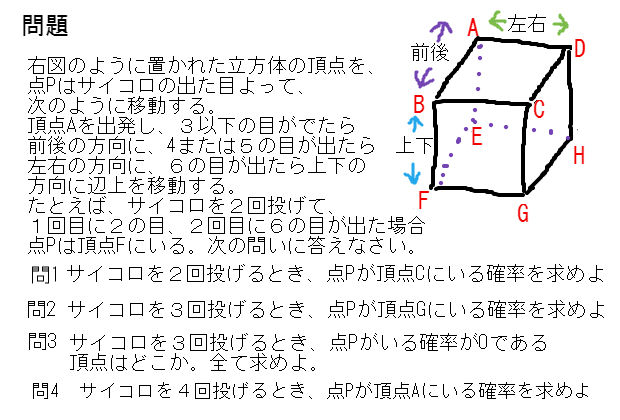



確率と経路の問題 やや難 制限5分 中学数学 理科 寺子屋塾の復習サイト
「または」 というキーワードに注目すると、 「和事象の確率」 であることがわかるね。 POINT ポイントにおける、「P(A)=目の和が4になる確率」、「P(B)=目の和が5になる確率」、「P(A∪B)=目の和が4または目の和が5の確率」として計算をしていこう。 確率 基本的な確率の問題練習プリントです。 確率とは ある事柄の起こりうることが期待される程度を表す数 サイコロを投げたとき、3が出る確率は6分の1になります。 *サイコロに何か細工をしない限り、サイコロのどの目の出方も同じに 16年4月9確率が苦手でかなり悩んでいることだろう。 確率 が苦手という高校生、受験生は非常に多い。 実は、微分や積分のような計算は大得意なのに、 確率 の問題になるとどうしても点を取れない受験生もいるのだ。 微積分などは、計算の意味・方法をひとたび理解してしまえば、あとはただ計算していくだけである。 しかし確率の問題には 特有の難しさ が存在し



確率 問題 中学




コンプリート 数学 確率 問題 ぬりえのベストコレクション
高校数学の基本問題 Gogle site →数ⅠA →数ⅡB →数Ⅲ (旧C) ***最近の更新*** 約数の個数,約数の総和 確率の入試問題 確率の漸化式(入試問題) 反復試行の確率(入試問題) 絶対値付き関数の定積分 Rの関数hist () Rの関数sample () 名義尺度データの比率の検定 フィッシャーの正確確率検定 高校数学A確率 教科書(問題・解答・公式・解説) 21年4月29日 このページでは、 数学A「確率」の教科書の問題と解答をまとめています。高校数学!確率の典型問題を解説します。 高校生からの質問 箱の中に赤い玉が5個、青い玉が3個、黄の玉が7個ある。 (1)3個の玉を取り出したとき、すべてが違う色である確率を求めよ。 (2)4個の玉を取り出したとき、赤い玉が他のどの玉よりも多い確率を求めよ。 上記の問題が分から




高校数学a 反復試行の確率 先にk回起こる 受験の月
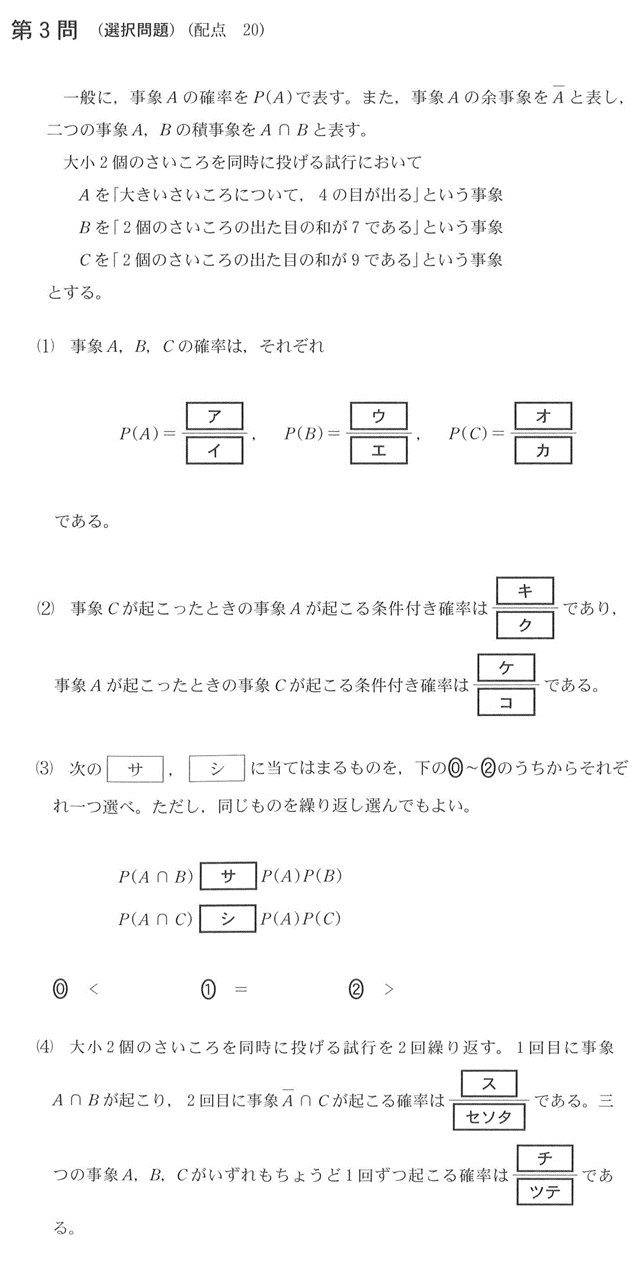



センター試験 場合の数と確率 の必勝テクニック 第3回 応用編 高校生3分ニュース 進研ゼミ高校講座
高校数学 解説動画 数学B 数列 Σ(シグマ)の計算① 2,158 views;入試問題 1696 都立青山高校16年度数学入試問題大問4解説 数学 数学で必ずやっておきたい復習チェックポイント&復習法 入試問題 160 都立日比谷高校16年度数学入試問題大問4解説確率 激ムズ⇒簡単やん! ? 公立高校入試 数学のポイント 投稿日時 19年1月18日 投稿者 nakatanijuku_edit いよいよ明石の公立高校受験まで後二ヶ月を切ってきました! 中谷塾でも過去問・予想問題などの演習を行っています。 その中で今回は数学解法のポイントをお伝えします!




高校数学無料問題集 数a 第1章 場合の数と確率 条件付き確率 桝 ます Note



数学 確率 茨城県公立高校入試問題
高校数学の無料プリント 実際に高校生の人たちから質問を受けた箇所を説明していきます。 まだまだ作りたでですが、徐々に充実させていきます。 質問と回答 目次 非表示 1 基本問題の解説プリン反復試行の確率2(n回以上の確率)に関する問題 映像授業 Try IT(トライイット) 548K subscribers Subscribe 高校 数学A 確率15 反復試行の確率2 (12分)3講 順列(1章 場合の数と確率) 問題集高校数学aです。わかりやすいポイントと例題つきの問題集です!定期テスト対策にお使いください。全て無料でダウンロードできます。塾や家庭教師、学校でご自由にお使いください!




様々な整数問題と確率 年札幌日大 高校入試 数学 良問 難問




高校数学の確率問題が苦手な人必見確率を完璧にする勉強法とは
4講 条件付き確率(2節 確率) 問題集高校数学aです。わかりやすいポイントと例題つきの問題集です!定期テスト対策にお使いください。全て無料でダウンロードできます。塾や家庭教師、学校でご自由にお使いください!高校数学 問題検索 数学A 場合の数と確率 「確率の基礎熊本大学 大学教育統括管理運営機構附属 数理科学総合教育センター/Mathematical Science Education Center 〒 熊本市中央区黒髪2401 全学教育棟A棟3階 (数理科学総合教育センター事務室)




高校数学a 反復試行の確率1 ちょうどn回の確率 例題編 映像授業のtry It トライイット



高校数学 問題検索 数学a 場合の数と確率 確率の基礎 数学
高校数学 数と式対称式はどんなとき使うんですか? 図形と計量正弦定理と余弦定理のどっちを使えばいいんですか? 整数の性質不定方程式ax+by=c(c≠0)の整数解を求めるときの式変形について 図形の性質チェバの定理(三角形の t1 t −1 人の中で一番好きな人」が先頭 k k k 人の中にいないと,その人と交際してしまい「全体の中で一番好きな人」までたどりつかない) よって,成功する確率は 1 n ∑ t = k 1 n k t − 1 = k n ( 1 k 1 k 1 ⋯ 1 n − 1) \dfrac {1} {n}\displaystyle\sum_ {t=k1}^ {n}\dfrac {k} {t1}\\ =\dfrac {k} {n}\left (\dfrac {1} {k}\dfrac {1} {k1}\cdots \dfrac {1} {n1}\right) n1



15年前期 千葉県公立高校入試 数学 第2問 4 確率 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




高校 数学 長文で複雑な問題を読み解く 確率など シンキングツール 思考ツール 授業案




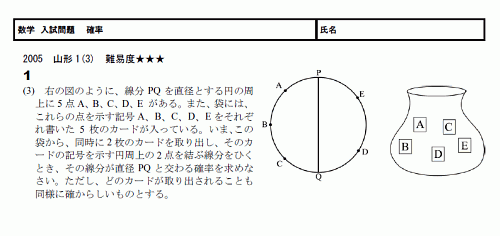
難関都立高校の確率問題 解いておきたい3つの練習問題 算数数学苦手克服 家庭教師のマスコンサルティング




面白い確率 集合写真は何枚撮れば全員の目が開いているのか 高校教師とictのブログ 数学 情報 Ict




確率13 原因の確率の導入例1 怜悧玲瓏 高校数学を天空から俯瞰する




高校受験対策 数学 確率 カード の問題 動画 19ch



高校数学確率の問題です この文が間違っている理由を教えてく Yahoo 知恵袋




高校入試 超効率問題集 数学 Amazon Com Books




確率 スタディーx



数学を分かりやすく考えてみようと試みるサイト 分かりやすい高校数学 確率 番外4 モンティ ホール問題3



教科書レベルの問題一覧と解答 数学a 場合の数と確率 教科書より詳しい高校数学




確率 激ムズ 簡単やん 公立高校入試 数学のポイント 明石の塾なら中谷塾




コンプリート 数学 確率 問題 ぬりえのベストコレクション



数学 確率確率の問題で5c3とかありますよね このcとはどういう意味なん Yahoo 知恵袋




確率の問題を間違えてしまう5つの原因と求め方とは 高校生向け受験応援メディア 受験のミカタ




高校数学 確率問題 センター試験 Spi対応 By Masunori Wada




順列と組合せの違いと例題 高校数学の美しい物語




令和2年度 年 灘高入試数学問題を解いてみた 東大合格コム




高校数学a 組合せ の確率2 応用 練習編 映像授業のtry It トライイット




高校数学 4step 数学a 全問解説 第1章 場合の数と確率 第1節 場合の数 2 場合の数 問題 22 35 カリスマ塾長 タイガーblog



確率問題全般 京極一樹の数学塾
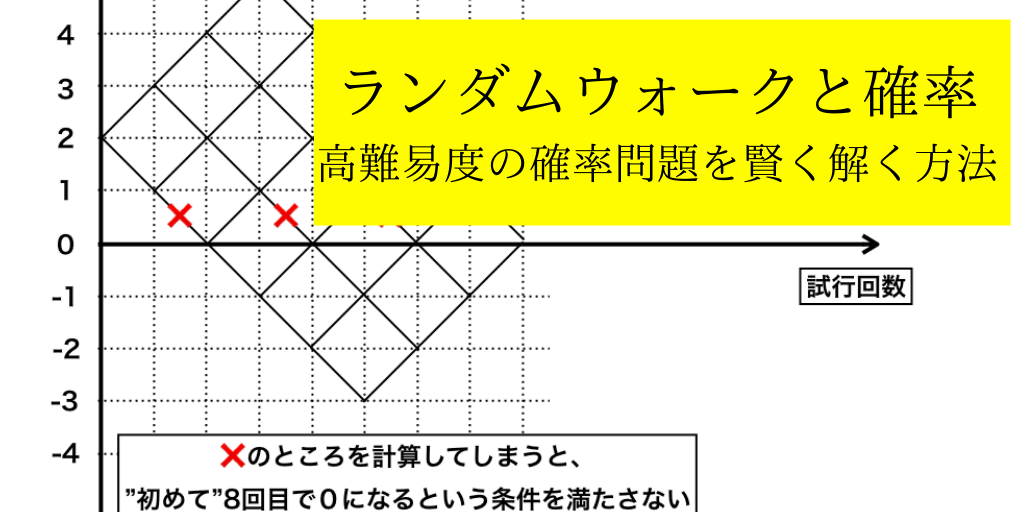



ランダムウォーク 酔歩 の意味と確率の問題の解法を分かりやすく解説



確率問題全般 京極一樹の数学塾




3講 順列 1章 場合の数と確率 問題集 高校数学a




確率の問題を間違えてしまう5つの原因と求め方とは 高校生向け受験応援メディア 受験のミカタ




問題5 確率が分かると円周率が計算できる Pythonで学び直す高校数学 エンジニアtype 転職type




高校数学 確率問題 苦手単元克服 センター試験 Spi 大学受験 公務員試験 就職試験対応 Para Android Apk Baixar




数学確率 高校入試問題で添付の確率の問題がわかりません 宜しくお願 高校受験 教えて Goo




確率の問題を間違えてしまう5つの原因と求め方とは 高校生向け受験応援メディア 受験のミカタ




確率の問題です Aのとき4通り Bのとき4通り だと思ったのですが Clear




高校入試 解き方 が身につく問題集 数学 Amazon Com Books




共通テスト 数学 予想問題演習 171 数学b 確率分布と統計的な推測の問題です 需要は少ないかもしれませんが 数学bの中では多分一番点が取りやすいです 共通テストでしか数学bを使わない人は学習をする価値があるかも そもそもこの分野で深い




確率と場合分け 17年度岐阜県 高校入試 数学 良問 難問




中学数学の確率の問題の解き方 コイン サイコロ くじ カード 数学fun




高校数学 確率 玉が登場する確率問題の解き方 数学の面白いこと 役に立つことをまとめたサイト




入試伝説 早稲田大学 トランプの確率 正しいのは 1 4 10 49 受験の月




4講 条件付き確率 2節 確率 問題集 高校数学a




高校数学 確率問題 苦手単元克服 センター試験 Spi 大学受験 公務員試験 就職試験対応 Para Android Apk Baixar



高校入試 数学 関数 確率 Sas 数学教室




18年度 神奈川県公立高校入試 標準問題 数学 問題 4 6




高校数学a じゃんけんの確率 N人のじゃんけん 受験の月




中学2年生 数学 確率 資料の活用 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




高校入試確率の傾向と対策 定番問題はマスターしよう 高校入試徹底対策ガイド




数学確率対策 大問先生の神奈川県公立高校入試問題攻略法 第二の家 ブログ 藤沢市の個別指導塾のお話



17年 北海道公立高校入試過去問 数学 標準 裁量問題 を画像で解説 家庭教師のsora




高校数学無料問題集 数a 第1章 場合の数と確率 条件付き確率 桝 ます Note




コインの確率の高校入試問題の解き方を超図解 Youtube




確率と場合分け 17年度岐阜県 高校入試 数学 良問 難問



U9j580gf8iba369ji2w Xyz Cat 15




年前期 千葉県公立高校入試 数学 第2問 4 確率 配点5点 問題 解答 解説 動画と文字両方あり 船橋市議会議員 朝倉幹晴公式サイト




17年度 北海道公立高校入試 標準問題 数学 問題 5 7




オリジナルの高校数学の問題を掲載していきます P 場合の数 確率




この問題の 2 と 3 がなぜこのような答えになるのか分かりません Clear




確率の求め方とは 高校数学aの解説記事総まとめ12選 遊ぶ数学



大学入試数学の問題




集合論と確率 問題演習 高校数学の例題解説 基本演習 6 Liberal Art S Diary




中学2年生 数学 確率 資料の活用 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




高校数学 数a 28 確率 じゃんけん編 Youtube




コンプリート 数学 確率 問題 ぬりえのベストコレクション




確率 スタディーx




答え サイコロの目の積と確率 Piececheck 17 17 東大数学9割のkatsuyaが販売する高校数学の問題集



確率 スタディーx




確率22 鯉のぼり問題 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学 数a 19 確率 さいころ編part 1 Youtube
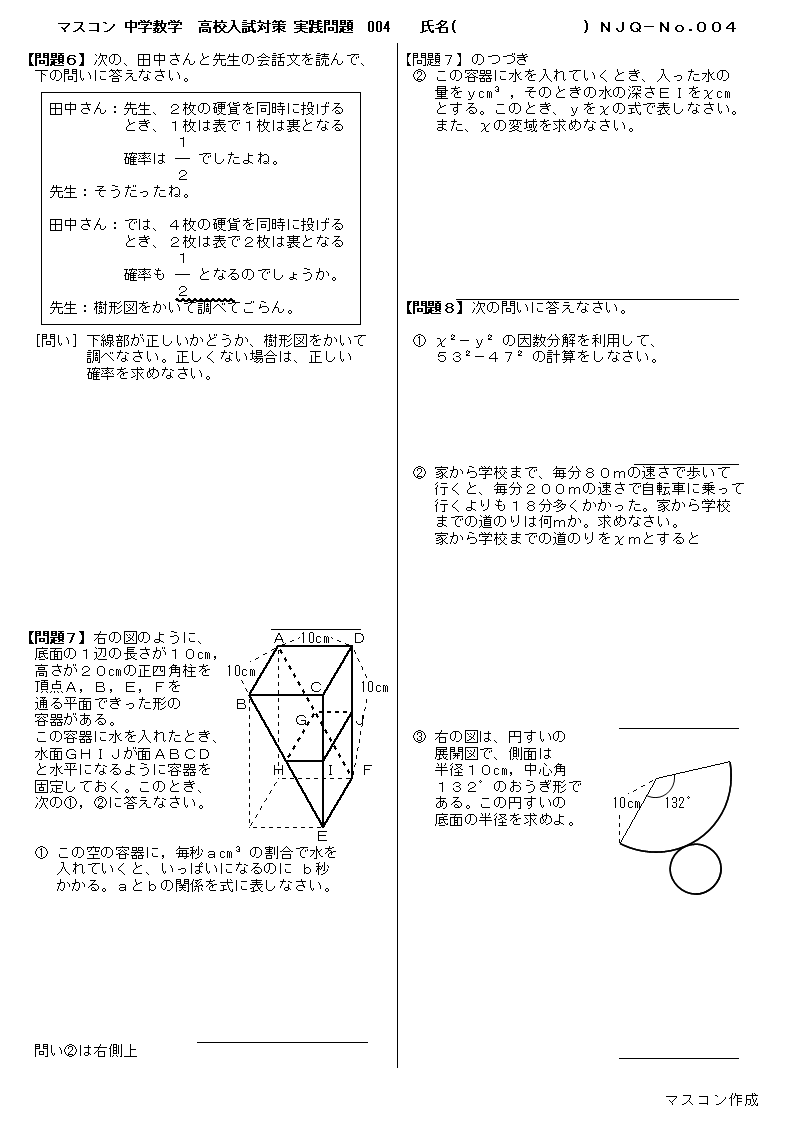



無料 中3数学 高校入試対策問題 問題プリント 333 実践問題 004




4講 条件付き確率 2節 確率 問題集 高校数学a




高校入試問題 数学 を毎日解いてみよう 18 H30 山口県 高校入試問題 数学 を解いてみよう




高校数学a 確率 教科書 問題 解答 公式 解説 学校よりわかりやすいサイト



今日の一問 確率 中学受験の人も 高校受験の人も チャレンジ ふるやまんの算数塾




順列の問題 一定の条件で並べる 高校数学の知識庫




サイコロの確率の練習問題 高校入試 中学数学 を難問まで難易度別に解説 坂田先生のブログ




高校数学復習記録 その7 桜花 現役バイト塾講師 Note




三重県の高校入試 数学の問題 H29前期 フロイデ学院



高校数学 問題検索 数学a 場合の数と確率 確率の基礎 数学




高校受験対策 数学 確率6の問題 動画 19ch




確率 硬貨を同時に投げるときの問題をパターンごとに解説 数スタ




確率 高校数学 3 原因の確率 身勝手な主張
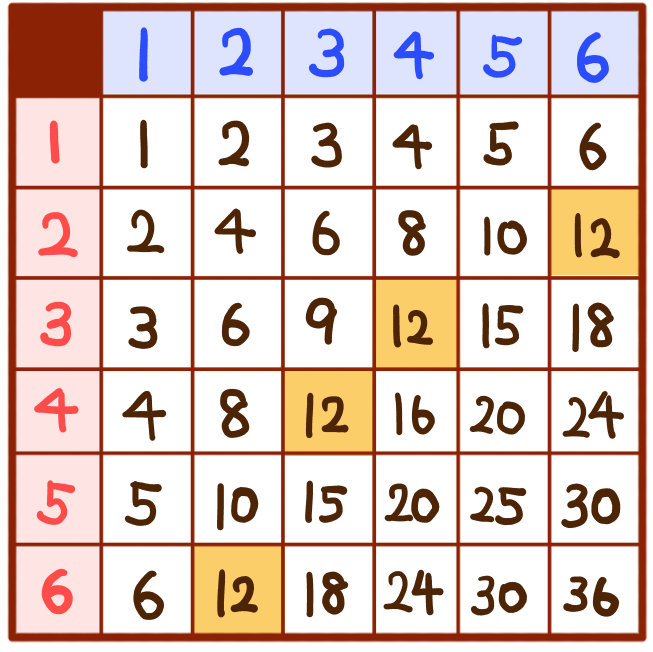



サイコロの確率の練習問題 高校入試 中学数学 を難問まで難易度別に解説 坂田先生のブログ



数学を分かりやすく考えてみようと試みるサイト 分かりやすい高校数学 確率 番外3 モンティ ホール問題2




中学数学 確率 高校入試でよく出る確率の応用問題をわかりやすく解説 数学の面白いこと 役に立つことをまとめたサイト




14年度 灘高等学校 Seraph Boy 渦巻く記憶 小学生当時 偏差値30代のライトノベル作家が入試問題を解くと




条件付き確率 の公式が感覚的に理解できる解説 練習問題 数学fun




コンプリート 数学 確率 問題 ぬりえのベストコレクション



底辺 高校 問題



高校数学学習サイト 高校無料問題




中学数学 確率 高校入試でよく出る確率の応用問題をわかりやすく解説 数学の面白いこと 役に立つことをまとめたサイト




教科書レベルの問題一覧と解答 数学a 場合の数と確率 教科書より詳しい高校数学




難関都立高校の確率問題 解いておきたい3つの練習問題 算数数学苦手克服 家庭教師のマスコンサルティング



高校 リード 問題 集 解答



高校 数学 問題


